
Greek Mythological Story of How Achilles Became a Warrior
So in the first instance, Achilles runs to where the tortoise was (10 metres away). But because the tortoise runs at 1/10th the speed of Achilles, he is now a further 1m away. So, in the second instance, Achilles now runs to where the tortoise now is (a further 1 metre). But the tortoise has now moved 0.1 metres further away.

7 Interesting Paradoxes in The World of Science UnBumf
During this time, the tortoise has moved only 8 meters. It will take Achilles 1 sec. more to run that distance, by which time the tortoise will have crawled 0.8 meters farther. Then it'll take Achilles 0.1 sec. to reach this third point while the tortoise moves ahead by 0.08 meters. And so on and so on. Thus, whenever Achilles reaches.

Achilles and the Tortoise YouTube
As explained in IEP's entry regarding Zeno's Paradox, current solution (aka Standard Solution) is based on the mathematics of the infinite, developed after 17th Century.. Current mathematical solution makes sense of an infinite sum having a finite amount.. This is not so for ancient mathematics and philosophy, as well as for Aristotle: either the quantities that we have to add are zero, in.

Achilles and the tortoise (AKIRESU TO KAME)
History. The origins of the paradoxes are somewhat unclear, but they are generally thought to have been developed to support Parmenides' doctrine of monism, that all of reality is one, and that all change is impossible [clarification needed]. Diogenes Laërtius, citing Favorinus, says that Zeno's teacher Parmenides was the first to introduce the paradox of Achilles and the tortoise.
Zeno's Paradox Achilles and the Tortoise Owlcation
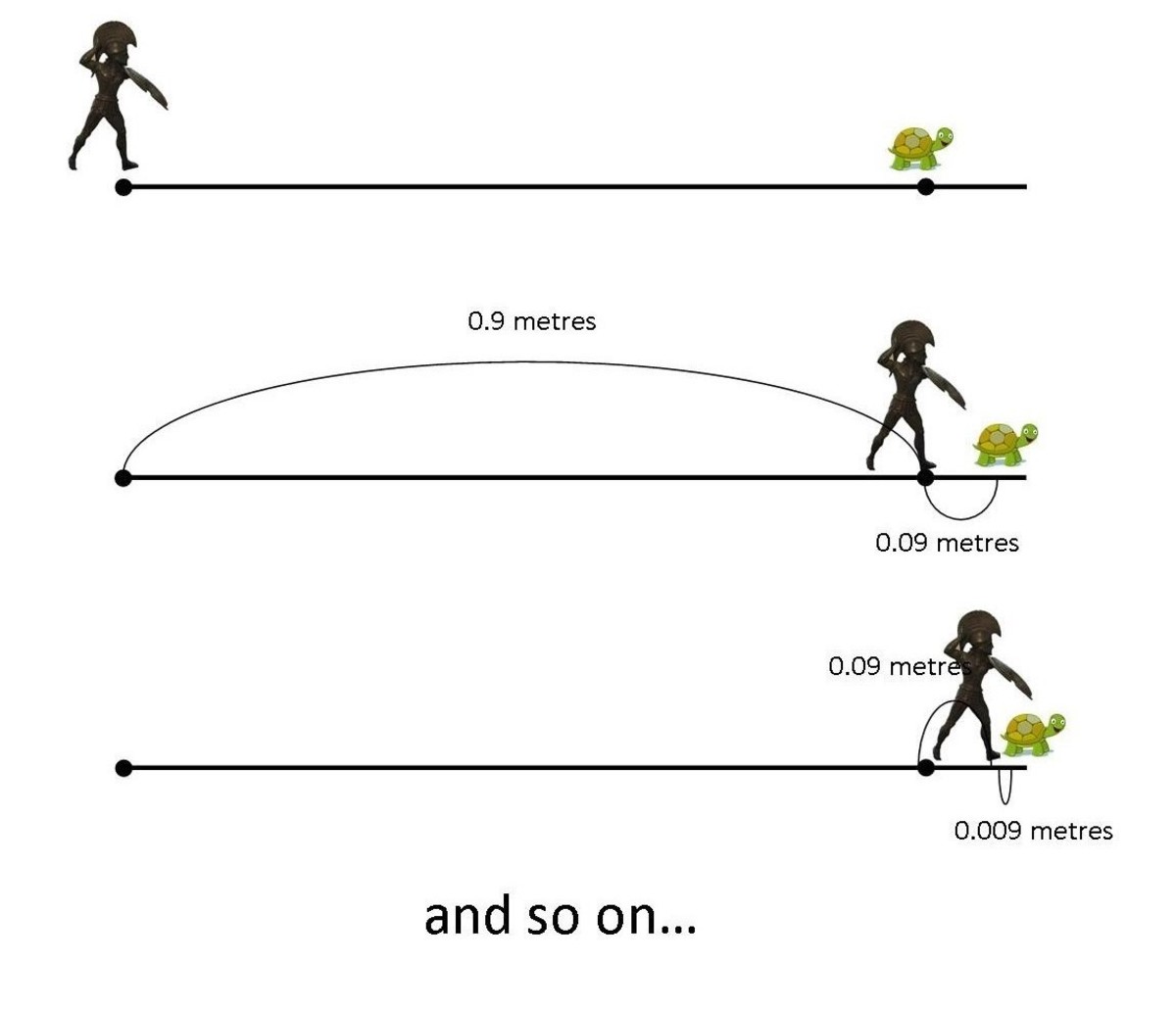
Zeno looks at this differently. In the time it takes Achilles to run the 0.9m to where the tortoise started, the tortoise will have travelled 0.09m. Achilles now runs this 0.09m, but the tortoise has travelled a further 0.009m. Achilles runs this only to find the tortoise has moved another 0.0009m ahead and so on for infinity.
Achilles and a turtle about infinite sequences Learning Driven
Achilles and the turtle stand at the starting line of the race for any finite distance. Achilles can run 2 times faster than the turtle, and therefore allows the turtle to move a certain distance from the start (we will call it d and assume it is smaller than 1/2 of the total distance). Achilles is running 2 times faster than the turtle, so.

Achilles and the Tortoise Paradox A Former Brilliant Member Brilliant
Ancient mathematical trickery proves that a mighty hero cannot overtake a tortoise (And that mortgages take a long time to pay off).(Part 1 of 6)Playlist lin.

Achilles and the tortoise Ancient World Magazine
Achilles the warrior is in a footrace with a tortoise, but Achilles has given the tortoise a 100-meter head start. If Achilles runs 10 times as fast as the tortoise, by the time he catches up to.

Achilles and the turtle——mathematical illusion|Dr.egg YouTube
If Achilles runs the first part of the race at 1/2 mph, and the tortoise at 1/3 mph, then they slow to 1/3 mph and 1/4 mph, and so on, the tortoise will always remain ahead. But don't tell your.

ACHILLES AND THE TORTOISE YouTube
In the first of a series on paradoxes, we take a look at Zeno's famous paradox of motion. Zeno argues that the Greek hero Achilles could never catch a tortoi.

Achilles and the Tortoise Achilles, Tortoise, The incredibles
See an explanation on Zeno's Achilles paradox, an infinite series concept used in finance to pay off mortgages. Know about the grandfather paradox and the concept of traveling back in time. Examine what is known about the ancient Athenian philosopher Socrates from Plato's dialogues and other sources. Learn about the six famous paradoxes in.

Achilles and the Tortoise Download Scientific Diagram
Achilles laughed louder than ever. "You will surely lose, my friend, in that case," he told the Tortoise, "but let us race, if you wish it.". "On the contrary," said the Tortoise, "I will win, and I can prove it to you by a simple argument.". "Go on then," Achilles replied, with less confidence than he felt before.

Achilles and the Turtle
Achilles paradox, in logic, an argument attributed to the 5th-century-bce Greek philosopher Zeno, and one of his four paradoxes described by Aristotle in the treatise Physics. The paradox concerns a race between the fleet-footed Achilles and a slow-moving tortoise.The two start moving at the same moment, but if the tortoise is initially given a head start and continues to move ahead, Achilles.

Achilles and the Tortoise 8 by DiscordQ on DeviantArt
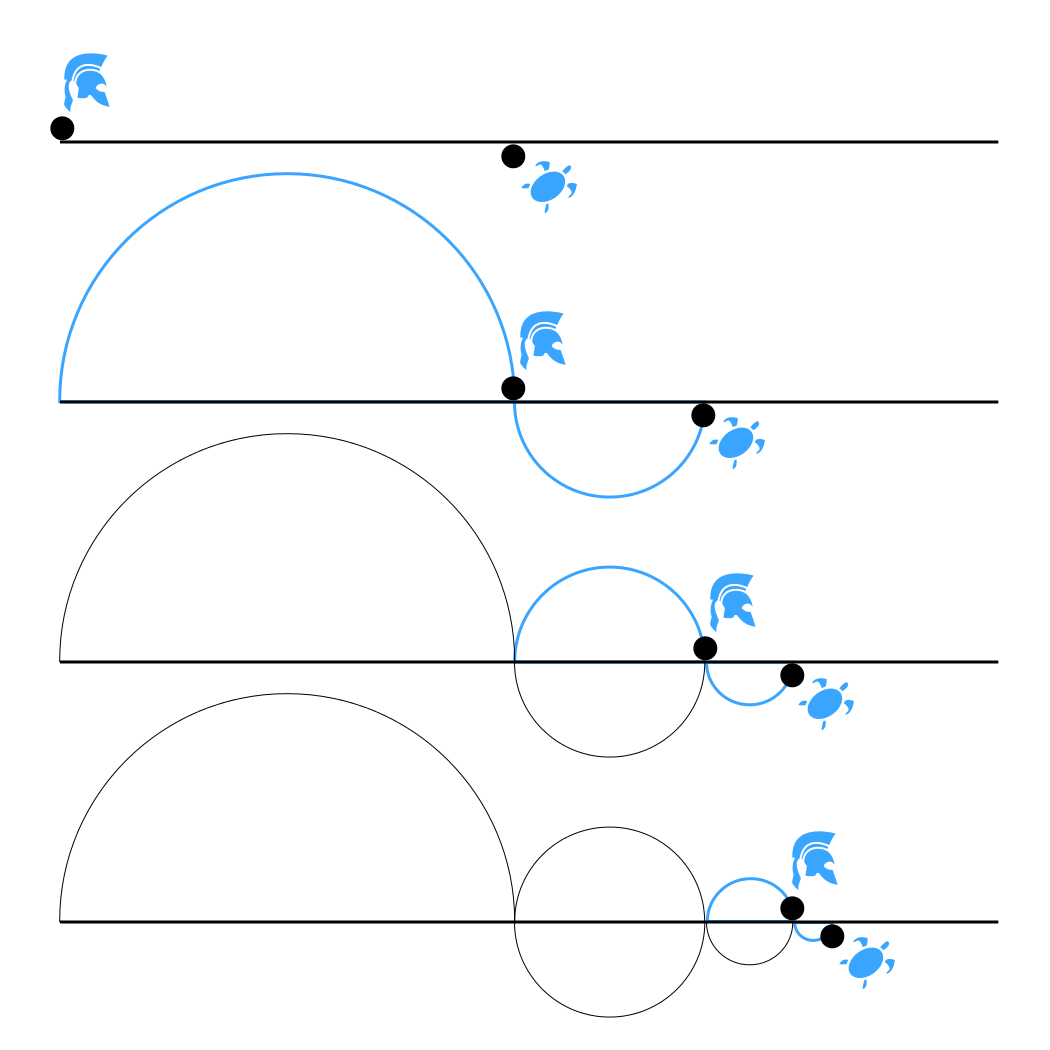
Once the race starts, in the time that Achilles will take to reach the starting position of the turtle, the latter will have moved forward by a distance d 1. Then Achilles will cover this distance d 1, but in the meantime the turtle will have covered another distance d 2. When Achilles reaches this new position, the turtle will have moved.

Achilles and a turtle about infinite sequences Learning Driven
Achilles travels a distance d 1 in reaching the point x 1 where the tortoise starts, but by the time Achilles reaches x 1, the tortoise has moved on to a new point x 2. When Achilles reaches x 2, having gone an additional distance d 2, the tortoise has moved on to point x 3, requiring Achilles to cover an additional distance d 3, and so forth.

Achilles and the Tortoise Mark Tansey The Broad
So in the first instance, Achilles runs to where the tortoise was (10 metres away). But because the tortoise runs at 1/10th the speed of Achilles, he is now a further 1m away. So, in the second instance, Achilles now runs to where the tortoise now is (a further 1 metre). But the tortoise has now moved 0.1 metres further away. And so on to infinity.