
The Easiest Guide to the 30 60 90 Triangle LifeSolved
A 30-60-90 day plan is a great way to help onboard new employees (or get an edge in an interview process) because it shows the key objectives for the first three months of employment. It aligns.
The Complete Guide to the 306090 Triangle [ult.edu.vn]
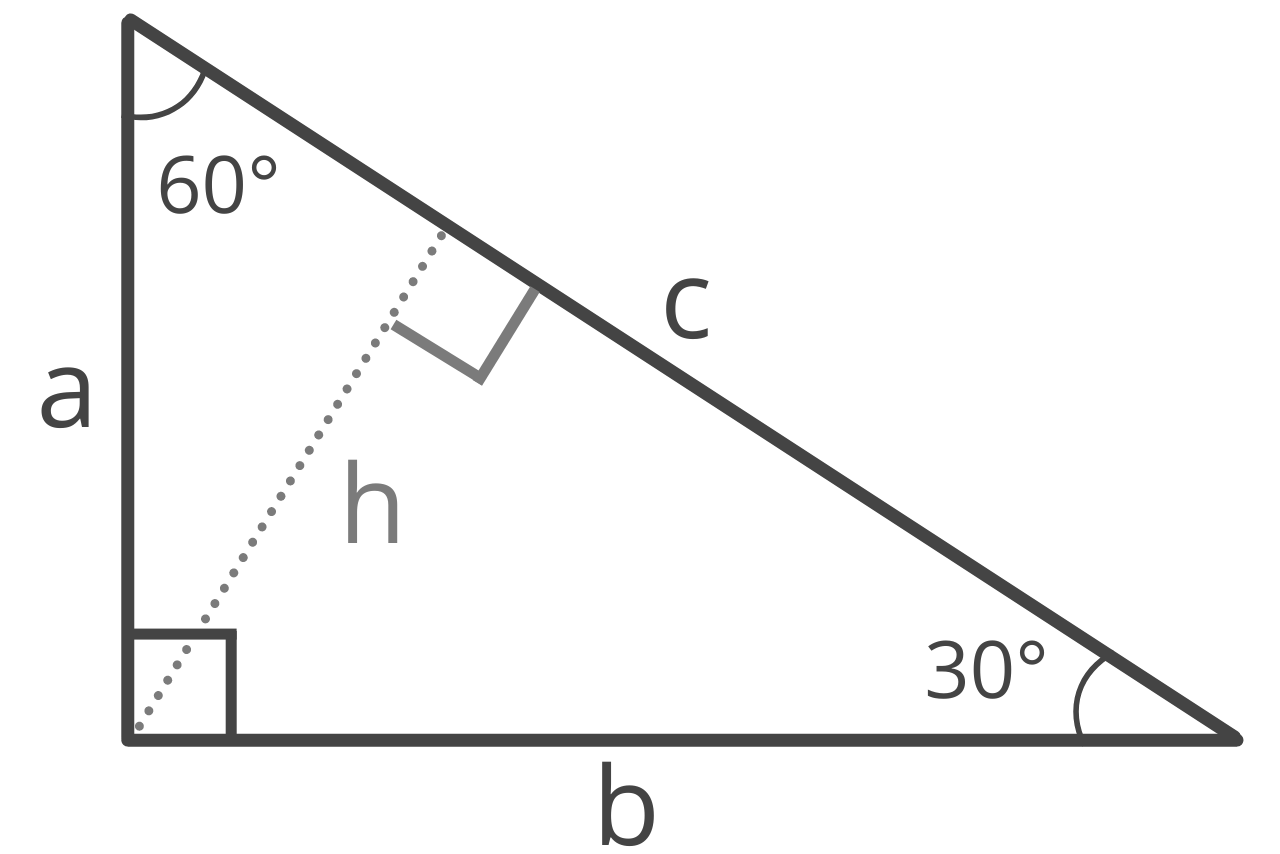
A 30-60-90 triangle is a right triangle having angles of 30 degrees, 60 degrees, and 90 degrees. For a 30-60-90 triangle with hypotenuse of length a, the legs have lengths b = asin(60 degrees)=1/2asqrt(3) (1) c = asin(30 degrees)=1/2a, (2) and the area is A=1/2bc=1/8sqrt(3)a^2. (3) The inradius r and circumradius R are r = 1/4(sqrt(3)-1)a (4) R = 1/2a. (5) The mean length of a line segment.

30 60 90 Day Plan Template [Free Powerpoint & Excel Template] AIHR
A 30-60-90 triangle is a special triangle since the length of its sides is always in a consistent relationship with one another. In the below-given 30-60-90 triangle ABC, ∠ C = 30°,∠ A = 60°, and ∠ B = 90°. We can understand the relationship between each of the sides from the below definitions:

60+30=90 YouTube
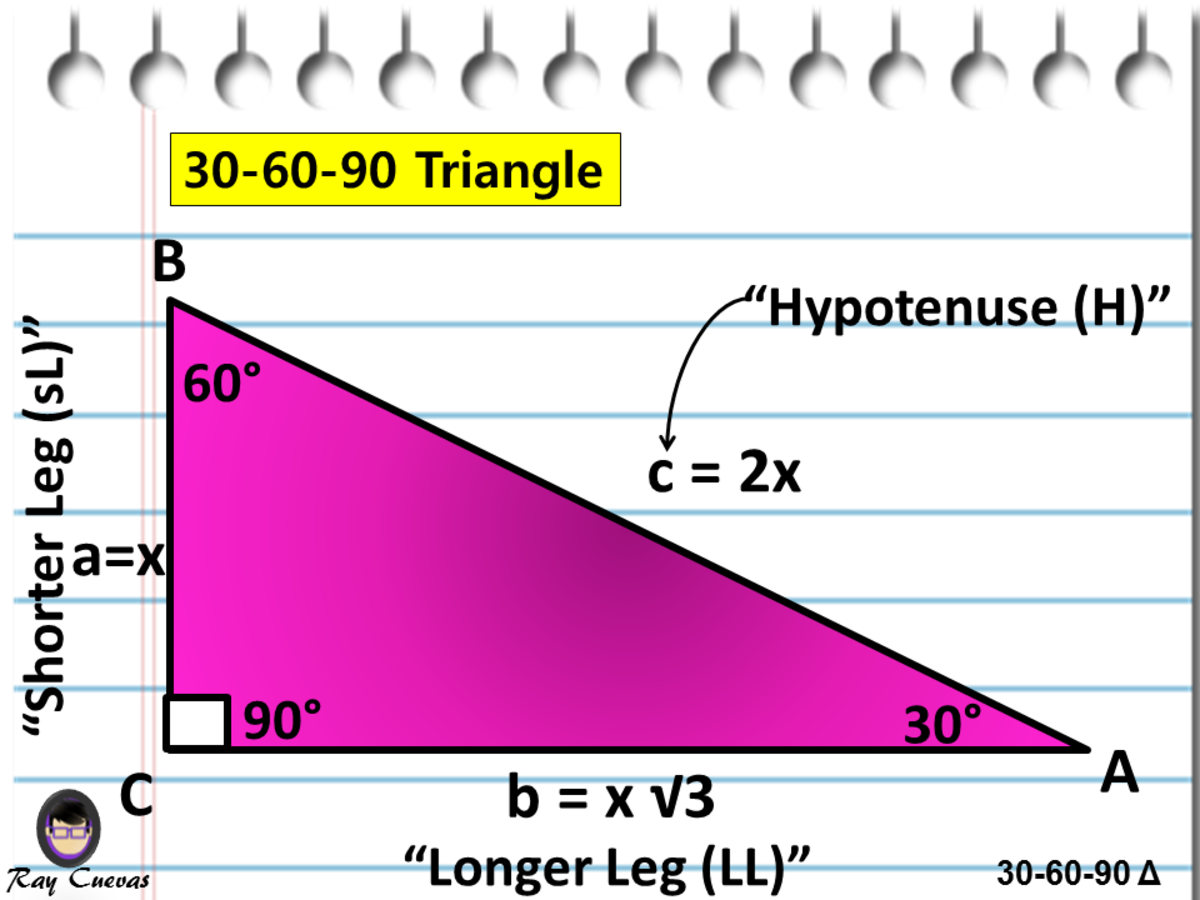
One of the two special right triangles is called a 30-60-90 triangle, after its three angles. 30-60-90 Theorem: If a triangle has angle measures 30∘ 30 ∘, 60∘ 60 ∘ and 90∘ 90 ∘, then the sides are in the ratio x: x 3-√: 2x x: x 3: 2 x. The shorter leg is always x, the longer leg is always x 3-√ x 3, and the hypotenuse is.
30 60 90 Triangle Calculator Formula Rules
When the hypotenuse of a 30 60 90 triangle has length c, you can find the legs as follows: Divide the length of the hypotenuse by 2. Multiply the result of Step 1 by √3, i.e., by about 1.73. The number you've got in Step 1 is the shorter leg of your triangle. The number you've got in Step 2 is the longer leg.
How To Find The Sides Of A 30 60 90 Triangle Vito Sibille
30°-60°-90° triangle: The 30°-60°-90° refers to the angle measurements in degrees of this type of special right triangle. In this type of right triangle, the sides corresponding to the angles 30°-60°-90° follow a ratio of 1:√ 3:2. Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known.

How To Make A 30 60 90 Day Plan 15 Templates To Download Free
A 30-60-90 triangle is a particular right triangle because it has length values consistent and in primary ratio. In any 30-60-90 triangle, the shortest leg is still across the 30-degree angle, the longer leg is the length of the short leg multiplied by the square root of 3, and the hypotenuse's size is always double the length of the shorter leg.

How To Calculate 30 60 90 Triangle PELAJARAN
A 30-60-90 triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle). Because the angles are always in that ratio, the sides are also always in the same ratio to each other. The side opposite the 30º angle is the shortest and the length of it is usually labeled as x. The side opposite the 60º angle has a.

30 60 90 Triangle Unit Circle
A 30-60-90 degree triangle is a special right triangle, so it's side lengths are always consistent with each other. The ratio of the sides follow the 30-60-90 triangle ratio: 1:2:\sqrt {3} 1: 2: 3. Short side (opposite the 30 degree angle) = x. Hypotenuse (opposite the 90 degree angle) = 2x. Long side (opposite the 60 degree angle) = x√3.

30 60 Degree Triangle Clipart Etc Images and Photos finder
With 45-45-90 and 30-60-90 triangles you can figure out all the sides of the triangle by using only one side. If you know one short side of a 45-45-90 triangle the short side is the same length and the hypotenuse is root 2 times larger. If you know the hypotenuse of a 45-45-90 triangle the other sides are root 2 times smaller.

30 60 90 Triangle Unit Circle
Out of all the other shortcuts, 30-60-90 is indeed a special Triangle. What is a 30-60-90 Triangle? It is a triangle where the angles are always 30, 60 and 90. As one angle is 90, so this triangle is always a right triangle. Thus, these angles form a right-angled triangle. Also, the sum of two acute angles is equal to the right angle, and these.

306090 Triangle Rules, Formula, Theorem, Sides, Examples
A special right triangle with angles 30°, 60°, and 90° is called a 30-60-90 triangle. The angles of a 30-60-90 triangle are in the ratio 1 : 2 : 3. Since 30° is the smallest angle in the triangle, the side opposite to the 30° angle is always the smallest (shortest leg). The side opposite to the 60° angle is the longer leg, and finally.

30 60 90 Triangle
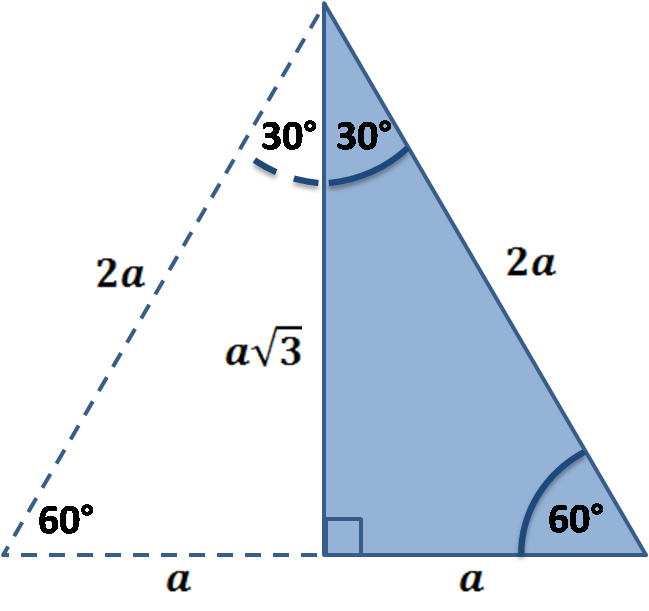
It is based on the fact that a 30°-60°-90° triangle is half of an equilateral triangle. Draw the equilateral triangle ABC. Then each of its equal angles is 60°. ( Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° angles. Then AD is the perpendicular bisector of BC ( Theorem 2 ).
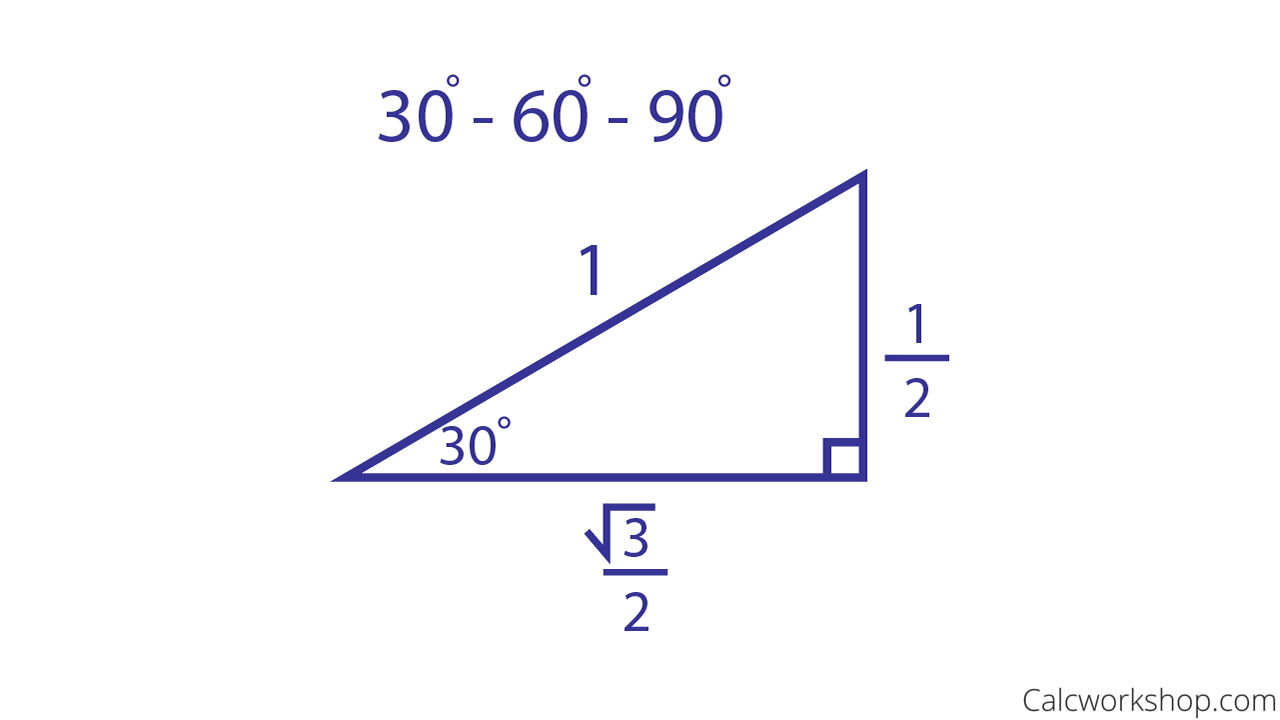
30 60 90 Triangles Worksheet
This video tutorial provides a basic introduction into 30-60-90 triangles. It explains how to find the value of the missing side of other triangles using th.

What Does A 306090 Day Plan Look Like? Supply Chain India Jobs
The ratio of the side lengths of a 30-60-90 triangle is 1 ∶ √3 ∶ 2. This means that if the shortest side, i.e., the side adjacent to the 60° angle, is of length 𝑎, then the length of the side adjacent to the 30° angle is 𝑎√3, and the length of the hypotenuse is 2𝑎. In this case we have 𝑎√3 = 15 ⇒ 𝑎 = 5√3.

Why did the 306090 triangle marry the 454590 triangle
Angle measures: The 60-30-90 triangle has one angle measuring 60 degrees, another measuring 30 degrees, and the other measuring 90 degrees. Side length ratios: The sides of the 60-30-90 triangle follow a ratio of 1:√3:2. The shorter leg (opposite the 30-degree angle) is half the length of the hypotenuse, while the longer leg (opposite the 60.