
Famous Irrational Numbers by tutorcircle team Issuu
Wikipedia The golden ratio doesn't arise only in geometry; in the Fibonacci sequence, where each number is the sum of the two previous ones (1, 1, 2, 3, 5, 8, 13, 21, 34,.), the ratios between.

What are Irrational Numbers? List, Properties, Arithmetic Operations
Catch a more in-depth interview with Ben Sparks on our Numberphile Podcast: https://youtu.be/-tGni9ObJWkCheck out Brilliant (and get 20% off) by clicking htt.

Irrational Numbers Visual Fractions
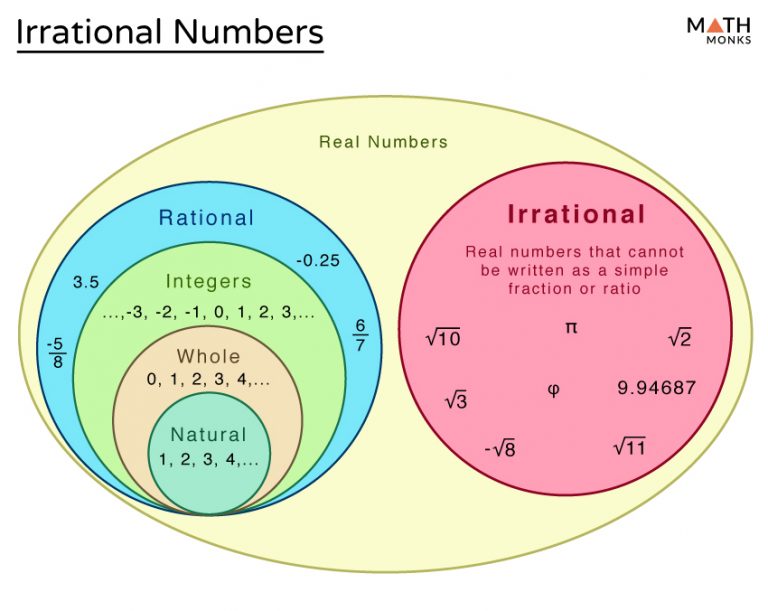
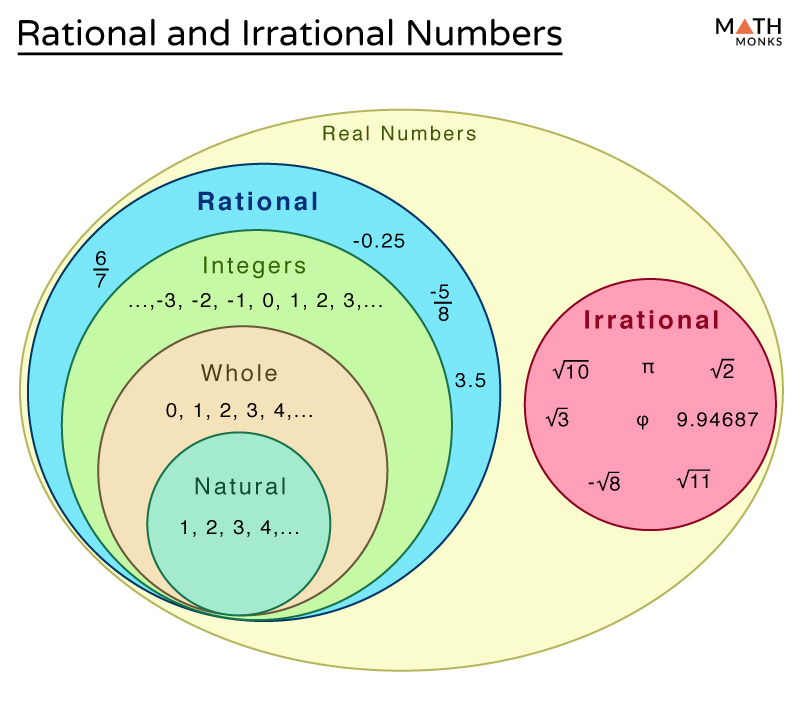
History Set of real numbers (R), which include the rationals (Q), which include the integers (Z), which include the natural numbers (N). The real numbers also include the irrationals (R\Q). Ancient Greece
Irrational Numbers Definition, Common Examples, & Diagram
An Irrational Number is a real number that cannot be written as a simple fraction: 1.5 is rational, but π is irrational Irrational means not Rational (no ratio) Let's look at what makes a number rational or irrational. Rational Numbers A Rational Number can be written as a Ratio of two integers (ie a simple fraction).

Rational And Irrational Numbers Worksheet
The number Φ is known as the golden ratio. Two positive numbers x and y, with x > y, are said to be in the golden ratio if the ratio between the sum of those numbers and the larger one is the same as the ratio between the larger one and the smaller; that is, x + y x = x y. Solution of (2.2.1) yields x / y = Φ.

2 The set of irrational numbers YouTube
The golden ratio's negative −φ and reciprocal φ−1 are the two roots of the quadratic polynomial x2 + x − 1. The golden ratio is also an algebraic number and even an algebraic integer. It has minimal polynomial. This quadratic polynomial has two roots, and. The golden ratio is also closely related to the polynomial.

PPT THE GOLDEN RATIO PowerPoint Presentation ID1744363
Wrath, Actually, Sal was saying that there are an infinite number of irrational numbers. And there is at least one irrational number between any two rational numbers. So there are lots (an infinite number) of both. And saying one thing that is infinite is more than another infinite thing is questionable because you can't add to infinite.

Irrational Numbers Definition and Examples Teachoo Irrational Nu
These measures reveal that the most irrational number, i.e. the one for which rational approximations perform the worst, is 1 plus the square root of 5 all divided by two - a figure roughly equal to 1.618. This number is already well known. It's called the "Golden Ratio".
What are Irrational Numbers? Definition and Explanation with Examples YouTube
So, for example, sqrt(2) is algebraic since it solves x²-2=0, and the golden ratio, (1+sqrt(5))/2, is algebraic since it solves x²-x-1=0. Knowing a number is algebraic gives us certain.

PPT IRRATIONAL NUMBERS PowerPoint Presentation, free download ID2731516
The common examples of irrational numbers are pi (π=3⋅14159265…), √2, √3, √5, Euler's number (e = 2⋅718281…..), 2.010010001….,etc. How do you know a number is Irrational? The real numbers which cannot be expressed in the form of p/q, where p and q are integers and q ≠ 0 are known as irrational numbers.

Irrational number divided by Rational number = ? YouTube
Going beyond the Golden Ratio. I show that for the same reason that the golden ratio, $\phi=1.6180334..$, can be considered the most irrational number, that $1+\sqrt {2}$ can be considered the 2nd most irrational number, and indeed why $ (9+\sqrt {221})/10$ can be considered the 3rd most irrational number. This blog post was featured on the.

Irrational Number Definition What It Is and How To Use It
An irrational number is a real number that cannot be written as a ratio of two integers. In other words, it can't be written as a fraction where the numerator and denominator are both integers. Irrational numbers often show up as non-terminating, non-repeating decimals. Learn more with our Intro to rational & irrational numbers video.

Irrational Numbers — Definition & Examples Expii
1 Answer. Sorted by: 9. The reason ϕ ϕ is sometimes called the "most irrational number" is because of its properties relating to continued fractions. A "continued fraction" is a nested fraction that goes on forever. Any number that can be expressed as a continued fraction is an irrational number. For example, the continued fraction for π π.

Irrational Numbers Definition And Examples Listten
The Most Irrational Number. Rational approximation of irrational numbers. The decimal expansion of an irrational number gives a familiar sequence of rational approximations to that number. For example since = 3.14159. the rational numbers. r 0 = 3, r 1 = 3.1 = 31/10, r 2 = 3.14 = 314/100,
Rational and Irrational Numbers Differences & Examples
Irrational numbers are numbers that cannot be expressed as the ratio of two whole numbers. This is opposed to rational numbers, like 2, 7, one-fifth and -13/9, which can be, and are, expressed as.

Irrational Numbers
The square root of two, aka √2, is irrational too, as is its sort-of (we'll get to that) neighbor √3. The square root of four, however, definitely isn't. An infinite decimal expansion of.